The Use of Formulas in Measurement

The Use of Formulas in Measurement

Figure A
A Proposed Backyard Patio

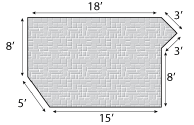Quite often school measurement activities focus heavily on using formulas such as A = L × W to find area of a rectangle or P = 2 × (L + W) to find the perimeter of a rectangle. People remember these formulas, and sometimes they even use them appropriately when they need to find a particular derived measurement. There are, however, numerous formulas to remember, and most people cannot recall all of the formulas that they learned in all their years of schooling. Many people can recall formulas that they learned by rote, but they do not know when to use them or whether they have any relevance to everyday life. More importantly, there are many times in our daily lives when we need to compute a measurement of a shape for which there is no formula. All of this suggests that perhaps school instruction has focused a bit too much on the importance of formulas in relation to measurement tasks. Figure A shows a portion of my backyard that I would like to pave with bricks or paving stones. I have measured each of the outside dimensions as shown. (Note: the dimensions are estimates that are rounded to the nearest whole foot.) How would I compute the number of bricks to buy? How would I compute the number of feet of perimeter lumber to buy? Obviously, this is not a problem for which you have learned a formula. An effective way to solve a problem such as this one is to decompose the shape into smaller parts and solve each part, as shown in the Figure B.

Figure B
Finding Patio Area

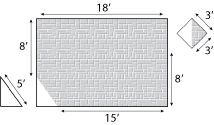We can move the upper triangle off to the side and calculate its area. This decomposing makes it clear that this triangle is one-half of a square, or 4.5 square feet. We can consider the lower left triangle as an area to be subtracted, since it does not receive paving stones. When we have it by itself we can see that its base must be 3 feet, because this portion plus the remaining 15 feet of the bottom of the patio must equal the top 18' of the patio. Calculating the height of this lower left triangle becomes the most challenging part of the problem. If we can determine its height, then we can use simple addition to find the height of the main rectangular part of the patio. Probably you remember something about the Pythagorean Theorem, which tells us that a² + b² = c². In this case a is 3, so a² is 9. c is 5, so c² is 25. Turning the formula around, we see that c² − a² gives us b², or 25 − 9 is 16. b² is 16, the square root of 16 is 4, so b must be 4 feet. Now we know that the rectangular part of the patio is 18 feet by 12 feet. 18 × 12 = 216, so the main part of the patio is 216 square feet. Using the height of 4, for this lower left triangle, we can see that its area is ¹⁄₂ of a 3-foot by 4-foot rectangle. Its area is therefore 6 square feet. After we subtract the lower left triangle (6 square feet) from the large rectangle (216 square feet) and add the upper right triangle (4.5 square feet), we will have the area of the patio (214.5 square feet). Our next step would be to determine how many bricks it takes to fill a square foot, divide our overall area by that amount, and then purchase that number of bricks.

All of this is meant to illustrate that real-life problems are a lot more complex than what we can solve in a straightforward way with the simple formulas learned in school. Measurement tasks require much more creative thinking than merely applying formulas. As teachers we need to be able to do this kind of creative problem solving, and we need to be able to teach it. We need to place our learning of formulas into a context that shows the limitations (and applications) of the formulas that we learn. Naturally, formulas are required in the course of solving complex, real-world problems, but they are not applied in simple ways.

Further enhance your math curriculum with more Professional Development Resources for Teaching Measurement, Grades K-5.