Problem-solving is a critical 21st Century and social-emotional skill
The "draw a picture" strategy is a problem-solving technique in which students make a visual representation of the problem. This resource will help you help your students learn how to employ a fundamental problem-solving strategy that is easily grasped by learners of all abilities.Looking for more resources on 21st Century skills and social-emotional learning? Find them in our FutureFit resources center.
Problem Solving: Draw a Picture
What Is It?
The draw a picture strategy is a problem-solving technique in which students make a visual representation of the problem. For example, the following problem could be solved by drawing a picture:
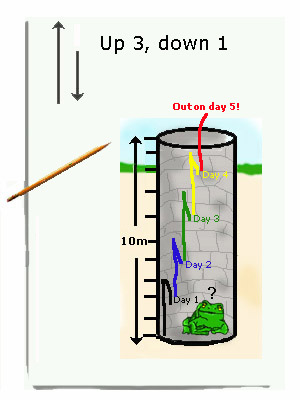
A frog is at the bottom of a 10-meter well. Each day he climbs up 3 meters. Each night he slides down 1 meter. On what day will he reach the top of the well and escape?
Why Is It Important?
Drawing a diagram or other type of visual representation is often a good starting point for solving all kinds of word problems. It is an intermediate step between language-as-text and the symbolic language of mathematics. By representing units of measurement and other objects visually, students can begin to think about the problem mathematically. Pictures and diagrams are also good ways of describing solutions to problems; therefore they are an important part of mathematical communication.
How Can You Make It Happen?
Encourage students to draw pictures of problems at the very beginning of their mathematical education. Promote and reinforce the strategy at all subsequent stages. Most students will naturally draw pictures if given the slightest encouragement.
Introduce a problem to students that will require them to draw a picture to solve. For example:
Marah is putting up a tent for a family reunion. The tent is 16 feet by 5 feet. Each 4-foot section of tent needs a post except the sides that are 5 feet. How many posts will she need?
Demonstrate that the first step to solving the problem is understanding it. This involves finding the key pieces of information needed to figure out the answer. This may require students reading the problem several times or putting the problem into their own words.
16 feet by 5 feet
1 post every 4 feet, including 1 at each corner
No posts on the short sides
Choose a Strategy
Most often, students use the draw a picture strategy to solve problems involving space or organization, but it can be applied to almost all math problems. Also students use this strategy when working with new concepts such as equivalent fractions or the basic operations of multiplication and division.